Permutasi dan Kombinasi
Permutasi (Permutations)
Permutasi adalah pengurutan Urutan penyusunan sekumpulan objek unik (tidak mengandung duplikasi); Permutasi dari sekumpulan n objek dapat diformulasikan sebagai faktorial dari n.
n! = n X (n-1)x(n-2)x(n-3)x...x3x2x1
kasus khusus
0! = 1
Permutasi: contoh 1
Berapa banyak kemungkinan cara untuk melakukan pengurutan angka pada baris pertama?
9! = 9 X 8 X 7 X 6 X 5 X 4 X 3 X 2 X 1 =362,880
Permutasi: formula
Permutasi pada pengurutan Urutan penyusunan sejumlah r objek yang diambil dari sekumpulan n objek unik dapat diformulasikan sebagai berikut
Permutasi: contoh 2
Berapa banyak kemungkinan cara untuk membentuk empat digit angka sebagai kode akses, di mana tidak boleh ada angka yang berulang?
n = 10
r = 4
Permutasi: contoh 3
Empat puluh tiga orang mengikuti lomba lari tingkat kecamatan. Berapa banyak kemungkinan posisi untuk juara pertama, kedua, dan ketiga yang dapat terbentuk ?
answer :
n = 43
r = 3
Permutasi: dengan duplikasi
Permutasi yang melibatkan kemunculan beberapa kali objek sejenis dapat diformulasikan sebagai berikut
Permutasi: contoh 4
Semisal kita dihadapkan pada sekumpulan deret huruf sebagai berikut: AAAABC
Berapa banyak cara untuk melakukan pengurutan deret huruf tersebut?
nA = 4
nB = 2
nC = 1
Permutasi: contoh 5
Sebuah perusahaan pengembang perumahan ditugaskan untuk melakukan pembangunan 6 unit rumah 1 lantau, 4 unit rumah 2 lantai, dan 2 unit rumah 3 lantai.
n1lt = 6
n2lt = 4
n3lt = 2
Bila setiap rumah dibangun secara berurutan, berapa banyak cara pengurutan bangunan rumah yang mungkin terbentuk ?
Kombinasi adalah pemilihan sejumlah r objek dari sekumpulan n objek tanpa memperhatikan urutan.
Kombinasi: contoh 1
Pemerintah kota memiliki 5 buah taman kota (A, B, C, D, E) yang membutuhkan instalasi lampu taman, Sayangnya anggaran yang tersedia hanya memungkinkan instalasi untuk 3 taman kota saja.
n = 5
r = 3
Berapa banyak opsi tiga taman kota yang bisa dipilih untuk instalasi lampu taman ?
ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE
Probabilitas dengan Permutasi & Kombinasi contoh 1
Suatu unit kegiatan mahasiswa beranggotakan 17 orang. Terdapat 3 orang yang menduduki posisi sebagai: ketua, sekretaris, dan bendahara, Setiap anggota memiliki kesempatan yang sama untuk menduduki ketiga posisi tersebut.
n = 17
r = 3
Berapa probability untuk memilih 3 orang anggota secara acak dan ketiganya menduduki posisi sebagai ketua, sekretaris, dan bendahara?

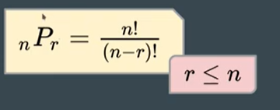










Komentar